Quick Sort
재귀를 이용하여 배열이 1개의 아이템이 남을때까지 분할 시키며 Pivot포인트를 지정하여 정렬한다.
Pivot
정렬 함수를 만들어 정렬을 실행할 아이템을 Pivot 포인트로 지정한다. 이후 배열의 아이템들을 순차적으로 Pivot과 비교하며 Pivot보다 낮은 아이템들은 배열의 왼편으로 이동시킨다. 배열의 모든 아이템들의 비교가 끝이나면 이동시킨 아이템들중 맨 오른쪽의 아이템과 Pivot의 위치를 교환한다. 이후 Pivot의 위치는 확정이 되며 Pivot을 기준으로 배열의 왼쪽 아이템들과 오른쪽 아이템들을 반복하여 진행한다.
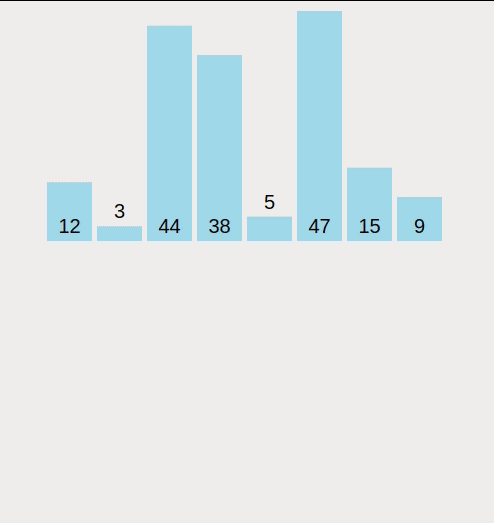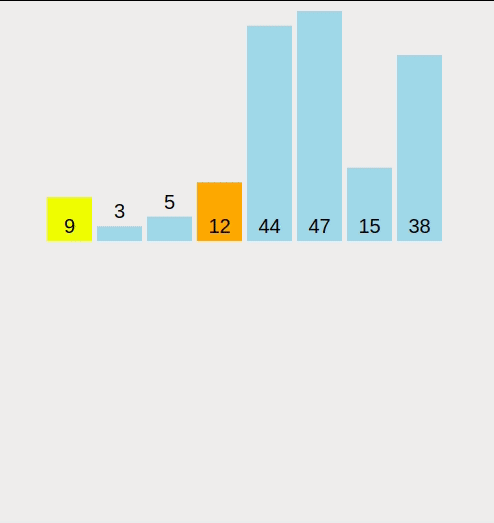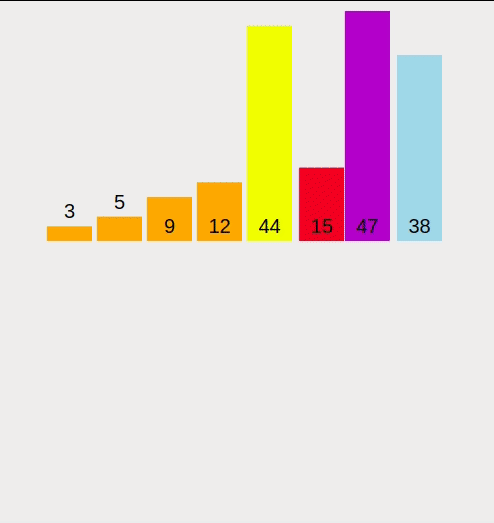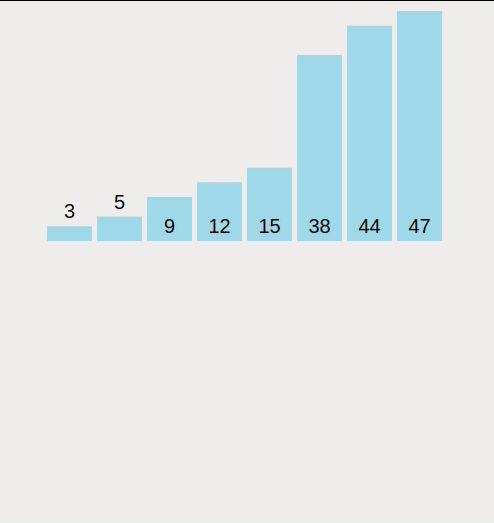
Pivot 함수
function pivot(arr, start = 0, end = arr.length - 1) {
let pivotIndex = start;
let swap;
for (let i = start + 1; i <= end; i++) {
if (arr[pivotIndex] > arr[i] || arr[pivotIndex] === arr[i]) {
pivotIndex++;
swap = arr[i];
arr[i] = arr[pivotIndex];
arr[pivotIndex] = swap;
}
}
swap = arr[pivotIndex];
arr[pivotIndex] = arr[start];
arr[start] = swap;
return pivotIndex;
}- pivot을 중심으로 좌측과 우측을 반복적으로 실행할 함수이므로 배열과 시작인덱스, 끝인덱스 이렇게 3개의 인수를 받는다.
- pivot의 인덱스를 저장할 변수와 배열의 정렬을 위한 변수를 설정한다.
- 처음 pivot을 배열의 첫 아이템부터 지정해주었다면 그 뒤의 아이템부터 순차대로 비교하는 반복문을 작성해준다.
- 조건문을 사용하여 비교대상의 값이 pivot의 값보다 더 높다면 그대로두고 더 낮거나 같다면 배열의 왼쪽 편으로 자리를 옴겨준다.
- 모든 반복문이 끝난후 pivot의 위치를 옮긴 아이템들과 안 옮긴 아이템들 사이로 위치시켜준뒤 pivot의 인덱스를 리턴해준다.
Quick Sort 로직
function quickSort(arr, left = 0, right = arr.length - 1) {
if (left < right) {
let pivotIndex = pivot(arr, left, right);
quickSort(arr, left, pivotIndex - 1);
quickSort(arr, pivotIndex + 1, right);
}
return arr;
}Quick Sort 함수도 마찬가지로 배열과 작업을 수행할 첫 index와 마지막 index를 인수로 받는다.
시작 인덱스가 마지막 인덱스보다 값이 낮다면 위에 만들어둔 pivot 함수를 먼저 돌리고 받은 pivot의 인덱스를 기준으로 좌측과 우측의 배열을 재귀함수로 돌린다.
Big O notation

최상과 평균 조건을 가정한다면 pivot을 기준으로 큰값들과 작은값들 반씩 나누게 되므로 만약 16개의 아이템을 하나의 아이템이 남을때까지 분해할경우 2*2*2*2 즉 4번의 작업을 수행하므로 O(log n)이 된다. 하지만 각각 분해 단계에서 배열의 아이템의 갯수 만큼 비교를 수행하므로 최종적으로 O(n log n)이 된다.
최악의 조건은 [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]과 같이 이미 정렬된 배열이 주어 젔을때 인데 분해 단계에서 16번의 작업을 수행하며 비교도 아이템의 갯수만큼 작업을 수행하므로 O(n²)이 된다.
이렇게 잘 정렬된 배열을 사용할경우 pivot을 지정할때 배열의 첫 아이템이 아닌 배열의 중간 아이템으로 정할경우 시간복잡도는 다시 O(n log n)이 된다.
'Datastructure & Algorithm' 카테고리의 다른 글
| Singly linked list (단일 연결 리스트) (0) | 2023.01.31 |
|---|---|
| Radix Sort (기수 정렬) 알고리즘 (2) | 2023.01.27 |
| Merge Sort(합병 정렬) 알고리즘 (0) | 2023.01.25 |
| 기본 정렬 알고리즘(Bubble, Selection, Insertion sorts) (0) | 2023.01.21 |
| 검색 알고리즘 (2) | 2023.01.18 |