단일 연결 리스트

위와 같은 구조이며 문자열, 숫자 등 무엇이던 원하는 데이터를 저장하는 자료구조중 하나이다.
배열처럼 순서에 따라 다수의 데이터를 저장하지만 인덱스없이 객체들이 연속으로 연결되있는 구조이다.
예를 들어 다섯번째 아이템에 접근하다고 가정햇을때 배열의 경우 인덱스를 이용하여 접근 할수 있지만 이경우에는 첫번째, 두번째, 세번째, 네번째 아이템들을 순차대로 거처야 다섯번째 아이템에 접근할수 있다.
class Node {
constructor(val) {
this.val = val;
this.next = null;
}
}
class SinglyLinkedList {
constructor() {
this.head = null;
this.tail = null;
this.length = 0;
}
}위의 코드와 같이 단일 연결 리스트에서는 아이템들을 노드로 부르며 각 노드들은 문자열이나 숫자와 같은 하나의 데이터와 다음 노드를 가르키는 정보를 담고 있으며 다음 노드가 없을경우 null을 표시한다.
또한 단일 연결 리스트는 시작노드인 head, 마지막노드인 tail 그리고 리스트의 길이의 정보를 가지며 SinglyLinkedList 클래스안에 method를 이용하여 함수를 작성하였다.
push() 메소드

push() 메소드는 리스트의 tail에 접근하여 자바스크립트 Array.push() 함수와 같이 데이터를 마지막부터 삽입시켜준다.
push(val) {
let newNode = new Node(val);
if (!this.head) {
this.head = newNode;
this.tail = newNode;
} else {
this.tail.next = newNode;
this.tail = newNode;
}
this.length++;
return newNode;
}
- value를 인자로받아 새 노드를 생성해준뒤 조건문을 이용하여 리스트의 head를 체크하여 리스트안에 노드가 있는지 확인한다.
- 만약 리스트안에 아무 노드도 들어있지 않다면 만든 노드를 리스트의 head와 tail에 저장해준다.
- 또한 리스트에 노드가 들어 있다면 마지막 노드의 다음 노드로 생성된 새로운 노드를 저장해주고 그 노드를 마지막노드로 설정해준다.
- 이후 리스트의 길이에 +1 해주면된다.
pop() 메소드

pop() 메소드는 head노드부터 시작하여 tail노드까지 추적후 Array.pop()과 같이 마지막 노드를 제거한뒤 그 이전 노드를 tail로 지정해준다.
pop() {
if (!this.head) return undefined;
let currentNode = this.head;
let preNode = currentNode;
while (currentNode.next) {
preNode = currentNode;
currentNode = currentNode.next;
}
this.tail = preNode;
this.tail.next = null;
this.length--;
if (this.length === 0) {
this.head = null;
this.tail = null;
}
return currentNode;
}
- 우선 조건문을 이용하여 빈 리스트일경우 undefined을 반환하여 작동을 중단 시킨다.
- 이후 현재 추적중인노드와 그 이전노드를 저장할 변수를 생성해준다.
- 반복문을 이용하여 추적중인 노드의 다음노드의 값이 null이 될때까지 preNode는 현재노드로 currentNode는 그다음노드로 저장해주며 한단계씩 앞으로 나간다.
- 마지막 노드에 접근했으면 preNode의 값을 리스트의 tail에 저장하고 저장된 tail의 다음노드의 값을 null로 저장하여 마지막노드와의 연결을 끊은 후 리스트의 길이를 -1 해준다.
- 모든작업 이후 리스트의 길이가 0이라면, 작업전 리스트의 노드는 한개만 존재했엇고 현재는 비어있는 리스트이므로 head와 tail을 null 값으로 없애준다.
shift() 메소드

리스트의 첫노드를 삭제해주는 메소드이며 Array.shift()와 동일한 기능이며 단일 연결 리스트에서 첫노드를 수정하는 작업의 경우 다른 노드들의 추적이 필요 없으므로 배열보다 좋은 성능을 가진다.
shift() {
if (!this.head) return undefined;
let preHead = this.head;
this.head = this.head.next;
this.length--;
preHead.next = null;
if (this.length === 0) this.tail = null;
return preHead;
}- 리스트에 노드가 존재하는지 확인후
- 작업 전의 첫 노드를 저장할 변수 생성 (삭제된 노드를 반환하지 않는다면 불필요)
- 이후 리스트의 head를 현재 head의 다음 노드로 지정해주고 리스트의 길이를 -1 해준다.
- 이후 삭제된 노드와 다음 노드간의 연결을 끊고
- 만약 모든 작업이후 리스트의 길이가 0 이라면 리스트의 마지막 노드의 정보도 지워준다.
unshift() 메소드

리스트의 첫노드에 데이터를 삽입해주는 작업이며 Array.unshift()와 비슷하지만 하나의 노드씩 추가가 가능하다.
unshift(val) {
let newNode = new Node(val);
newNode.next = this.head;
this.head = newNode;
this.length++;
if (this.length === 1) this.tail = newNode;
return newNode;
}- 받은 인자값을 이용하여 새 노드를 생성한다.
- 생성된 새 노드의 다음노드로 현재 리스트의 head와 연결시킨다.
- 이후 현재 리스트의 head를 생성된 새 노드로 지정해준뒤 리스트의 길이를 +1해준다.
- 모든 작업 이후에도 리스트의 길이가 1이라면 비어있던 리스트인 것이므로 리스트의 tail에도 새 노드를 지정해준다.
get() 메소드

인덱스를 인자로 받으며 받은 인덱스에 위치한 노드를 찾는 메소드
get(index) {
if (this.length - 1 < index || 0 > index) return null;
let currentNode = this.head;
for (let i = 0; i < index; i++) currentNode = currentNode.next;
return currentNode;
}- 인덱스의 값이 0보다 작거나 리스트의 길이를 넘어가는경우 null을 반환하고 함수를 종료한다.
- 리스트의 헤드를 현재위치로 변수에 저장
- 반복문을 사용하여 받은 인덱스만큼 반복하며 설정한 변수에 현재위치의 다음 노드를 반복하여 저장한다.
- 이후 현재 저장된 노드를 반환
set() 메소드
데이터값과 인덱스를 인자로 받으며 받은 인덱스에 해당하는 노드의 값만을 교체해준다.
set(val, index) {
let currentNode = this.get(index);
if (!currentNode) return false;
else currentNode.val = val;
return true;
}- 위에 작성한 get() 메소드와 받은 인덱스를 이용하여 변경하려는 노드를 찾는다.
- 노드를 찾았다면 그 노드의 데이터를 인자로 받은 데이터로 교체해 준다.
insert() 메소드
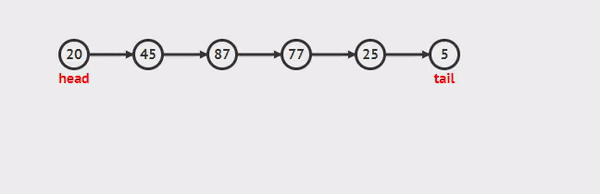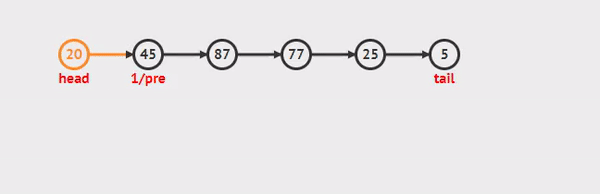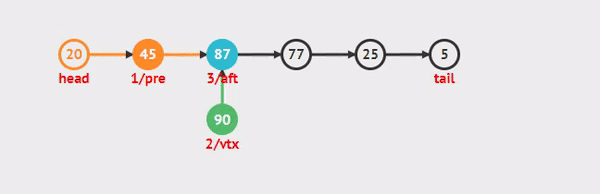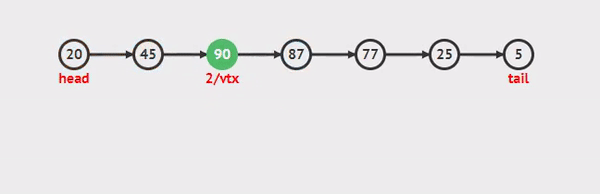
데이터값과 인덱스를 인자로 받으며 받은 인덱스의 자리에 새로운 노드를 삽입해준다.
insert(val, index) {
if (this.length < index || 0 > index) return false;
if (index === this.length) this.push(val);
else if (index === 0) this.unshift(val);
else {
let preNode = this.get(index - 1);
let currentNode = preNode.next;
let newNode = new Node(val);
newNode.next = currentNode;
preNode.next = newNode;
this.length++;
}
return true;
}- 인자로 받은 인덱스값의 범위가 알맞지 않다면 false를 반환
- 만약 인덱스값이 0이라면 위에 작성한 unshift()메소드를 호출, 인덱스값이 리스트의 길이와 같다면 push()메소드를 호출한다.
- 위의 상황이 모두 아니라면 get()메소드를 이용하여 받은 인덱스에 위치한 노드와 그 이전 노드를 찾아 변수에 저장,
- 이후 인자로 받은 데이터를 이용하여 새로운 노드를 생성해준뒤 변수로 저장한 노드들과 새로생성한 노드를 순서에 맞게 연결해주고 리스트의 길이를 +1 해주면 된다.
remove() 메소드

인덱스를 인자로 받으며 해당하는 위치의 노드를 제거한다.
remove(index) {
if (this.length < index || 0 > index) return undefined;
if (index === this.length) return this.pop();
else if (index === 0) return this.shift();
let preNode = this.get(index - 1);
let removedNode = preNode.next;
preNode.next = removedNode.next;
removedNode.next = null;
this.length--;
return removedNode;
}- 인자로 받은 인덱스의 값이 알맞는지 확인 후
- 받은 인덱스의 값이 0이라면 shift(), 리스트의 길이와 같다면 pop() 메소드들을 호출
- 위의 상황이 모두 아니라면 get()메소드를 이용하여 인덱스에 위치한 노드와 그 이전 노드를 변수로 저장하고
- 이전 노드의 다음노드로 인덱스에 위치한 노드의 다음노드를 연결한다.
- 이후 리스트의 길이를 -1해주고 변수에 저장된 연결이 해제된 노드의 다음노드를 지워준뒤 반환해준다.
reverse() 메소드
리스트의 모든 노드들의 순서를 반전시키는 메소드이다.
reverse() {
let currentNode = this.head;
this.head = this.tail;
this.tail = currentNode;
let next;
let pre = null;
for (let i = 0; i < this.length; i++) {
next = currentNode.next;
currentNode.next = pre;
pre = currentNode;
currentNode = next;
}
return this;
}현재노드와 이전과 다음노드들을 저장할 3개의 변수가 필요하다.
- 변수 currentNode에 현재 노드인 head를 저장
- 이후 리스트의 head와 tail을 바꿔준다.
- 리스트 길이만큼 반복문을 돌리며 변수 next에 현재노드의 다음노드를 저장한후 현재노드의 다음노드로 변수에 저장된 이전노드를 연결해준다.
- 이후 이전노드를 가르키는 변수 pre는 현재노드로, 현재노드 currentNode는 다음노드로 지정해준다.
Big O notation

삽입
단일 연결 리스트의 삽입 작업의 경우 리스트의 head와 tail을 불러와 새로 생성된 노드에 연결후 head와 tail의 정보를 업데이트 해주면 끝이난다. 이경우 시간복잡도는 O(1)이 된다.
하지만 배열의 첫 아이템에 새로운 데이터를 추가해줄경우 배열의 모든 데이터의 인덱스들을 옴겨주는 작업이 필요하므로 O(n)이 된다.
중간에 데이터를 삽입시켜줄경우 배열과 단일 연결 리스트의 경우 그 데이터의 위치에따라 시간 복잡도가 달라지기 때문에 O(n)이 된다.
삭제
단일 연결 리스트의 경우 0번째 노드를 삭제할때에는 리스트의 head만 연결을 해제하고 두번째 노드를 head로 등록해주면 되므로 O(1)이 된다. 하지만 마지막 노드를 삭제할때에는 마지막 노드의 이전 노드까지 추적이 필요하므로 O(n)이 된다.
반면 배열의 경우 반대 결과과 나타난다. 0번째 아이템을 삭제할때에는 O(n), 마지막 아이템을 삭제할때에는 O(1)이며 중간의 아이템을 삭제할때에는 배열과 연결 리스트 모두 아이템의 위치에따라 시간 복잡도가 달라지기 때문에 O(n)이 된다.
탐색 및 접근
연결 리스트의 경우 특정한 노드를 찾기위해선 그노드에 연결된 앞의 노드들을 추적하며 따라가야하므로 O(n)이 된다. 하지만 배열의 경우 인덱스만으로 임의 접근이 가능하기때문에 O(1)이 되며 탐색에 대해서는 배열이 효율이 좋다.
정리하자면 단일 연결리스트가 삽입과 삭제의 경우 배열에 비해 성능이 우수하다. 만약 삽입과 삭제 작업을 주로하거나 탐색작업이 필요하지 않는경우 혹은 그냥 주어진 순서대로 데이터를 관리하는 경우 단일 연결 리스트가 적절할 것이다.
'Datastructure & Algorithm' 카테고리의 다른 글
| Stack & Queue 자료구조 (0) | 2023.02.01 |
|---|---|
| Doubly Linked List (이중 연결 리스트) (0) | 2023.01.31 |
| Radix Sort (기수 정렬) 알고리즘 (2) | 2023.01.27 |
| Quick Sort (퀵 정렬) 알고리즘 (0) | 2023.01.26 |
| Merge Sort(합병 정렬) 알고리즘 (0) | 2023.01.25 |