Tree Traversal
트리가 가지고있는 모든 노드를 순회하는 알고리즘으로 모든 트리구조에서 사용할수 있다.
Breadth First Search(너비 우선 탐색)과 Depth First Search(깊이 우선 탐색)이 사용된다.
Breadth First Search(너비 우선 탐색)
root부터 시작하여 가로방향인 형제 노드들을 먼저 탐색하는 알고리즘이다.
Queue를 이용하며 기본적인 작동원리는 큐의 첫번째 아이템의 자식노드들을 순서대로 큐에 추가해주고 큐의 값을 새로운 배열에 넣어준뒤 큐에서 제거한다. 이후 큐에 아이템이 없어질때까지 반복하면된다.
BFS(node, queue = [], result = []) {
if (!node) return result;
result.push(node.val);
queue.shift();
if (node.left) queue.push(node.left);
if (node.right) queue.push(node.right);
return this.BFS(queue[0], queue, result);
}이경우 처음 순회 탐색을 시작하려는 노드를 받아 자체적으로 꼬리재귀를 실행하였으며 순서만 조금 바꼇을뿐 기본적인 작동원리는 같다.
- Base case를 설정해준뒤 받은 노드의 값을 새 배열에 추가, 이후 dequeue를 해준다.
- 받은 노드값의 자식노드들을 enqueue해주며 반복하여 작동시킨다.
Depth First Search(깊이 우선 탐색)
너비 우선 탐색과 달리 세로방향으로 탐색을 실시한다.
대표적으로 Inorder, Preorder, Postorder가 있다.
Inorder

제일 왼쪽의 노드 부터 시작하여 그의 부모노드를 거치며 탐색한다.
이진 탐색 트리에서 이 방식을 사용하면 데이터의 크기가 작은 순서로 정렬된다.
DFSInOrder(node, result = []) {
if (!node) return;
this.DFSInOrder(node.left, result);
result.push(node.val);
this.DFSInOrder(node.right, result);
return result;
}
// result = [11, 20, 29, 32, 41, 50, 65, 72, 91, 99]- 재귀를 위한 Base case를 작성해준다.
- 먼저 받은 노드의 왼쪽 자식노드부터 재귀를 실행한뒤 배열에 노드의 값을 차례로 저장한다.
- 이후 오른쪽 자식노드를 재귀로 돌리면 된다.
Preorder
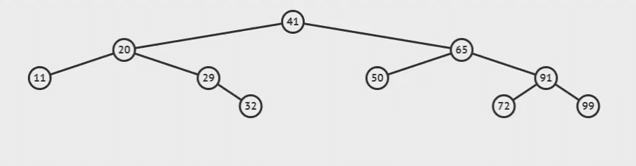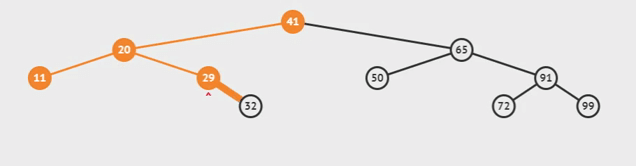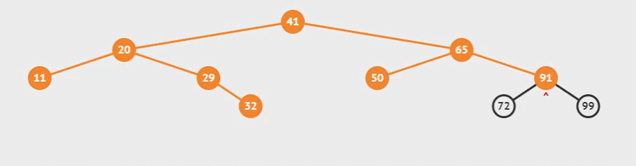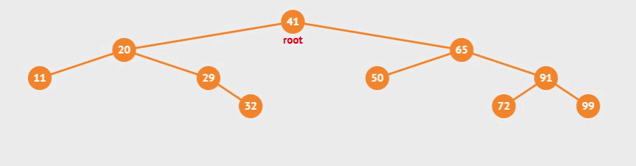
Inorder와 진행방향은 같지만 root부터 시작하여 지나는 모든 노드들을 순서대로 정렬한다.
DFSPreOrder(node, result = []) {
if (!node) return;
result.push(node.val);
this.DFSPreOrder(node.left, result);
this.DFSPreOrder(node.right, result);
return result;
}
// result = [41, 20, 11, 29, 32, 65, 50, 91, 72, 99]Inorder와 코드는 같지만 해당 node의 값을 재귀 이전에 저장해준다.
Postorder
root를 기준으로 한쪽 부터 시작하며 leaf 노드부터 시작하며 다른 leaf들을 찾아 탐색한다. 이후 해당 부모가 가지고 있는 모든 leaf들의 탐색이 끝나면 그 부모 노드의 탐색까지 마친다. 이후 root를 기준으로 반대편도 동일하게 진행하며 root를 마지막으로 탐색을 마친다.
DFSPostOrder(node, result = []) {
if (!node) return;
this.DFSPostOrder(node.left, result);
this.DFSPostOrder(node.right, result);
result.push(node.val);
return result;
}
// 위 애니메이션들과 같은 트리를 사용할시
// result = [11, 32, 29, 20, 50, 72, 99, 91, 65, 41]
마찬가지로 코드는 같지만 해당 노드의 값을 모든 재귀 이후에 저장해준다.
마무리
모든 순회들의 시간복잡도는 O(n)이다. 하지만 사용에 따라 공간 복잡도가 달라진다.
BFS(Breadth First Search)의 경우 모든 노드를 저장하기 위해 큐를 사용한다. 만약 사용하는 트리의 너비가 넓을수록, 즉 균형잡힌 트리일수록 더 많은 데이터를 큐에 집어 넣어야 하기때문에 DFS(Depth First Search)보다 효율이 떨어진다.
DFS의 경우 재귀 사용으로 인하여 균형잡히지 않은 트리 일수록 콜스택에 쌓이며 이경우에는 BFS가 공간복잡도의 효율이 더 증가 할수도 있다.
이진 탐색 트리를 사용한다면 DFS의 Inorder의 경우 데이터의 값을 순서대로 정렬할때, Preorder일 경우에는 루트부터 흐름의 순서대로 저장 되기때문에 데이터를 어딘가에 저장해 놧다가 나중에 복원해야 하는 상황이 있을때 사용하는 것이 좋을것 같다.
'Datastructure & Algorithm' 카테고리의 다른 글
| 그래프 (Graphs) (0) | 2023.03.19 |
|---|---|
| Binary Heap(이진 힙)과 Priority Queue(우선순위 큐) (0) | 2023.02.14 |
| Binary Search Tree (이진 검색 트리) (0) | 2023.02.08 |
| Stack & Queue 자료구조 (0) | 2023.02.01 |
| Doubly Linked List (이중 연결 리스트) (0) | 2023.01.31 |