이진 검색 트리를 알기 위해선 트리 구조와 이진 트리 구조를 알아야 한다.
Tree (트리)
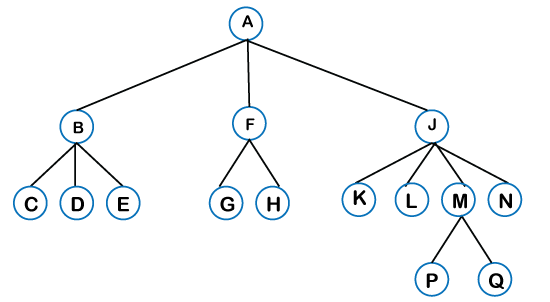
연결 리스트 처럼 노드로 이루어진 데이터 구조로 parent와 child 노드로 이루어저 있다.
연결 리스트는 한노드당 하나의 노드만을 한줄로만 연결 시키지만 트리의 경우 하나의 노드와 다른 여러 노드들로 연결시켜 여러갈래로 구성된다.
트리의 경우 몇가지 규칙을 가지고 있다.
부모노드는 여러 자식노드를 가질수 있지만 자식노드는 하나의 부모 노드만을 가지며 부모노드는 자식 노드만을 가리킬수 있다.
또한 트리의 시작점은 단하나의 노드에서 시작되며 이 노드를 root라 부른다.
몇가지 용어들을 더 정리 하자면
| 자식노드 | 루트에서 멀어지는 방향으로 연결된 노드 |
| 부모노드 | 자식노드와 반대의 개념 |
| 형제노드 | 같은 부모를 가진 노드들 |
| 리프 | 자식이 없는 노드 |
| 엣지 | 노드간의 연결 (그림의 선과 화살표가 이에 해당) |
Binary Tree (이진 트리)
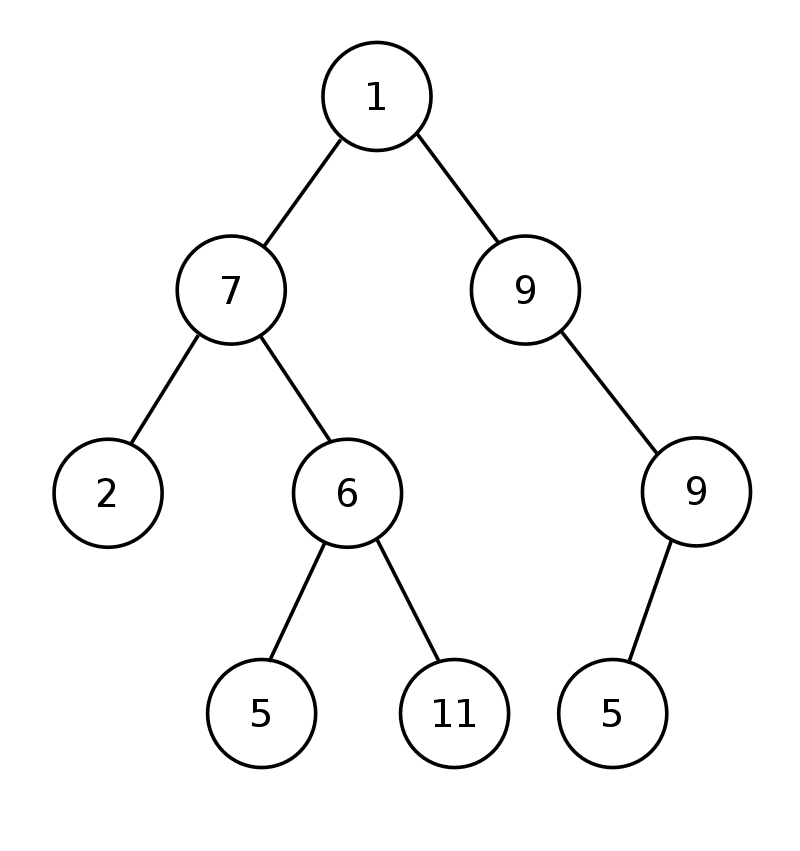
트리와 비슷하지만 하나의 부모 노드는 최대 두개의 자식노드만을 가질수 있으며 데이터들을 규칙없이 저장한다.
Binary Search Tree (이진 검색 트리)
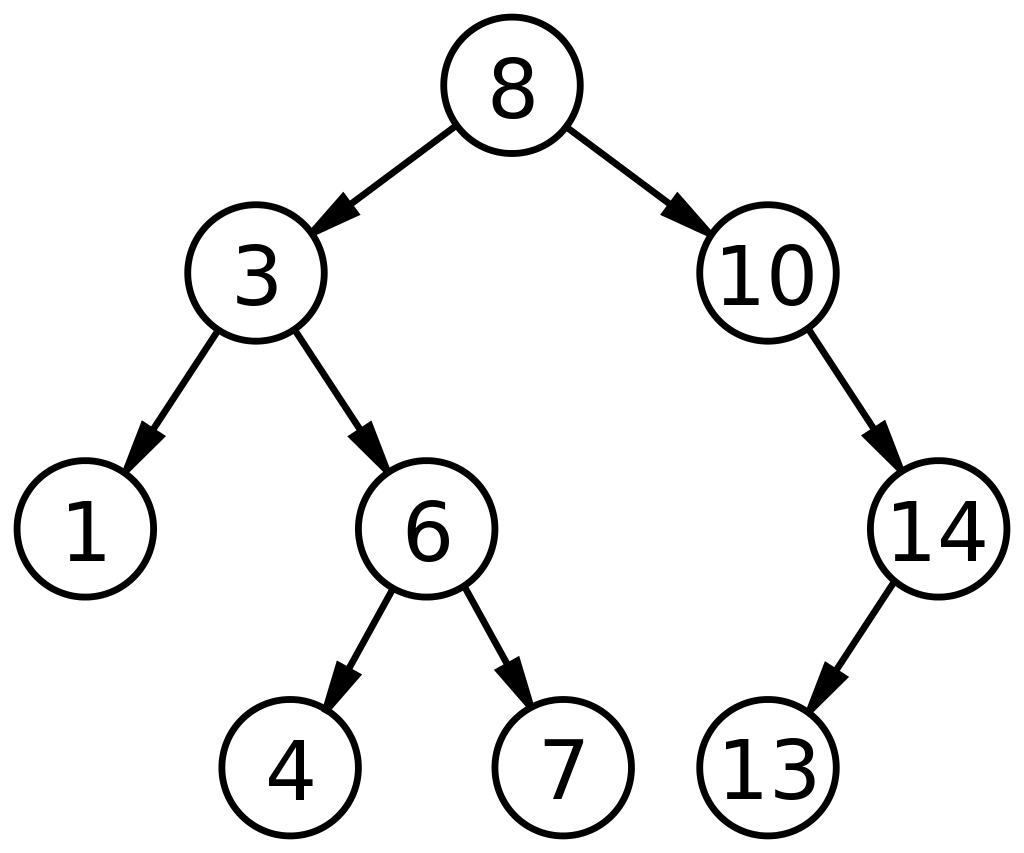
이진 트리와 비슷하지만 데이터들을 비교해서 정렬 가능하게 저장한다.
부모노드의 왼쪽에 있는 모든 자식노드들은 언제나 부모노드보다 작고 오른쪽은 크다. 또한 중복된 노드값을 허용하지 않는다.
class Node {
constructor(val) {
this.val = val;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor() {
this.root = null;
}
}앞서 말한것처럼 이진 탐색트리는 root라는 시작점을 가지며 각 노드들은 각자의 고유한 데이터를 가지며 자식노드와의 데이터값을 비교하여 자신의 왼쪽과 오른쪽으로 정렬시킨다.
insert() 메소드

루트를 시작하여 비교후 한단계씩 내려가며 마지막에 비교할 대상이 없을 경우 자신의 노드를 맨끝 (leaf)에 추가한다.
insert(val) {
let newNode = new Node(val);
if (!this.root) this.root = newNode;
else {
let currentNode = this.root;
while (currentNode.left !== newNode && currentNode.right !== newNode) {
if (val === currentNode.val) return undefined;
if (val < currentNode.val) {
if (!currentNode.left) currentNode.left = newNode;
else currentNode = currentNode.left;
}
if (val > currentNode.val) {
if (!currentNode.right) currentNode.right = newNode;
else currentNode = currentNode.right;
}
}
}
return this;
}- 노드를 생성한뒤 트리에 root가 있다면 반복문을 이용하여 연산을 시작한다.
- 만약 추가하려는 값이 현재노드(자신의 부모가 될 노드)와 비교하여 값이 크다면 right로 작다면 left로 보낸다.
- 만약 다음 노드가 존재한다면 그노드와도 값을 계속해서 비교해준다.
- 반복문 도중 자신과 같은 값의 노드를 찾으면 undefined을 반환, 만약 leaf(맨 끝 노드)까지 도달햇다면 그자리를 자신의 자리로 저장해준다.
find() 메소드

insert와 작동 방식이 매우 비슷하며 루트를 시작으로 밑으로 추적하여 노드를 삽입 시키는 대신 원하는값을 찾아낸다.
find(val) {
if (!this.root) return undefined;
let currentNode = this.root;
while (currentNode.val !== val) {
if (currentNode.val < val) {
if (!currentNode.right) return undefined;
currentNode = currentNode.right;
}
if (currentNode.val > val) {
if (!currentNode.left) return undefined;
currentNode = currentNode.left;
}
}
return currentNode;
}insert()메소드와 굉장히 비슷하다.
root부터 시작하여 부모노드들과 계속해서 비교하며 내려가며 자신의 값을 찾으면 그 값을 반환한다.
remove() 메소드

여러가지 경우의 수가 존재한다.
1. 제거하려는 대상이 leaf인 경우
1-1. 해당 트리에 root만 존재할경우
1-2. 그 대상이 부모노드의 왼쪽에 위치한 경우
1-3. 그 대상이 부모노드의 오른쪽에 위치한 경우
2. 제거하려는 대상의 오른쪽에 자식노드가 있을 경우
2-1. 제거하려는 대상의 다음 근사값(successor)이 자신의 자식노드인 경우 (만약 애니메이션에서 20번 노드를 삭제할때 이에 해당)
2-2. successor가 자신의 자식노드가 아닌경우
2-2-1. 찾은 successor에 자식노드가 있을경우 (위의 애니메이션이 이에 해당)
3. 제거하려는 노드의 왼쪽에만 자식노드가 있을경우
4. 제거하려는 노드가 root인 경우
remove(val) {
if (!this.root) return false;
let currentNode = this.root;
let parent;
let successor;
let successorParent;
// 노드가 존재하는지 체크후 제거하려는 노드와 그 부모노드 찾기
while (currentNode.val !== val) {
if (currentNode.val < val) {
if (!currentNode.right) return false;
parent = currentNode;
currentNode = currentNode.right;
}
if (currentNode.val > val) {
if (!currentNode.left) return false;
parent = currentNode;
currentNode = currentNode.left;
}
}
// Case1: 제거하려는 노드에 자식 노드가 없을경우
if (!currentNode.right && !currentNode.left) {
if (!parent) this.root = null;
else if (parent.val < val) parent.right = null;
else if (parent.val > val) parent.left = null;
return true;
}
// Case2: 제거하려는 노드의 오른쪽에 자식노드가 있을경우
else if (currentNode.right) {
successor = currentNode.right;
successorParent = currentNode;
while (successor && successor.left) {
successorParent = successor;
successor = successor.left;
} // get successor and its parent
successor.left = currentNode.left;
if (successorParent.val !== currentNode.val) {
let successorRight = successor.right;
successor.right = currentNode.right;
if (successorRight) {
successorParent.left = successorRight;
} else successorParent.left = null;
}
}
// Case3: 제거하려는 노드의 왼쪽 자식노드만 있을경우
else if (currentNode.left) {
successor = currentNode.left;
}
// 제거하려는 대상이 root 노드일경우와 아닐경우
if (!parent) this.root = successor;
else if (parent.val < val) parent.right = successor;
else if (parent.val > val) parent.left = successor;
return true;
}
}시작
먼저 find() 메소드와 같이 반복문을 돌려 제거하려는 노드와 그 부모 노드를 찾는다. ( find() 메소드를 호출하지 않은 이유는 부모노드도 찾아야 하기 때문 )
Case1: 제거하려는 노드에 자식 노드가 없을 경우
- 만약 부모노드도 없다면 그 트리는 root만 존재하므로 root를 없애준다.
- 해당 노드의 위치에따라 부모노드에서 지워주면 된다.
Case2: 제거하려는 노드의 오른쪽에 자식노드가 있을 경우
- 먼저 successor(제거하려는 노드보다 높지만 제일 근사한 값)과 그의 부모노드를 찾는다.
- 제거하려는값의 왼쪽 노드를 successor의 왼쪽 노드로 연결 (successor의 왼쪽은 존재할수 없기 때문에 확인해줄 필요가 없다.)
- 제거하려는 노드의 자식노드가 successor가 아닐 경우 successor의 오른쪽노드를 변수로 저장한뒤 제거하려는 노드의 오른쪽노드를 successor의 오른쪽노드로 이동시킨다.
- 이후 successor의 오른쪽노드를 저장한 변수에 값이 있다면 successor의 부모의 왼쪽노드에 연결 시켜주고 그렇지 않을 경우 successor의 부모의 왼쪽노드는 비워둔다.
Case3: 제거하려는 노드의 왼쪽 자식노드만 있을경우
- 이경우 successor는 존재 하지않으므로 predecessor(대상의 이전 근사값)만 찾아준다. (코드에서는 간편하게 successor로 같은 변수를 사용해주었다.)
마무리
마지막 단계에서는 이미 조합된 successor 혹은 predecessor를 제거하려는 값의 부모노드에 연결해주면된다.
만약 부모노드가 없다면 그 노드는 root가 되므로 root에 successor를 등록해주면 된다.
Big O notation
삽입, 삭제, 탐색의 평균 시간복잡도는 O(log n)으로 굉장히 효율이 좋다.
하나의 값을 추가하거나 찾을때 혹은 삭제할때 각 노드당 두가지의 선택이 주어진다. 현재 비교하는 노드보다 크거나 작은 값만을 연산하고 한쪽이 선택된 이후에 다른 한쪽의 모든 노드들은 그 경우의 수에서 모두 제외된다. 그렇기에 트리의 높이가 높을수록 경우의 수에서 제외되는 노드의 수도 증가하게 된다.
다만 트리의 형태가 링크드 리스트와 비슷하다면 즉 자식노드의 값들이 극단적으로 계속해서 증가하거나 계속해서 줄어든다면 O(n)의 결과를 가저온다. 이런경우 이진 탐색 트리 외의 다른 알고리즘을 사용하거나 트리의 루트를 중간값으로 바꾸어 사용한다.
'Datastructure & Algorithm' 카테고리의 다른 글
| Binary Heap(이진 힙)과 Priority Queue(우선순위 큐) (0) | 2023.02.14 |
|---|---|
| Tree Traversal (트리 순회), BFS, DFS (0) | 2023.02.08 |
| Stack & Queue 자료구조 (0) | 2023.02.01 |
| Doubly Linked List (이중 연결 리스트) (0) | 2023.01.31 |
| Singly linked list (단일 연결 리스트) (0) | 2023.01.31 |