Binary Heap
힙은 트리의 한 종류로 힙자체로도 많은 종류가 있다. 그중 하나가 바이너리 힙이며 이진 탐색 트리와 비슷하지만 조금 다른 규칙을 가지고 있다.
최대 이진 힙을 예로들어 부모노드는 항상 자식 노드보다 큰 값을 가지며 자식노드들 간의 순서가 존재 하지 않는다. (최소 이진 힙의 경우 부모노드는 항상 자식 노드보다 작은 값을 가짐) 또한 항상 최적의 용량을 가진다. 즉 자식노드가 생성되기 전에 모든 형제노드들이 채워지며 균형잡힌 트리구조로 만들어 진다. 그리고 항상 왼쪽의 자식 노드 먼저 채워지게 된다.
이진힙의 데이터들을 그 순서대로 배열에 나열할경우 어떠한 데이터의 인덱스가 n이라면 그의 왼쪽자식의 인덱스는 2n+1, 오른쪽 자식은 2n+2의 인덱스를 가지게 된다. 반대로 (n-1)/2이후 소수점을 버리면 그 노드의 부모노드의 인덱스를 구할수있다.
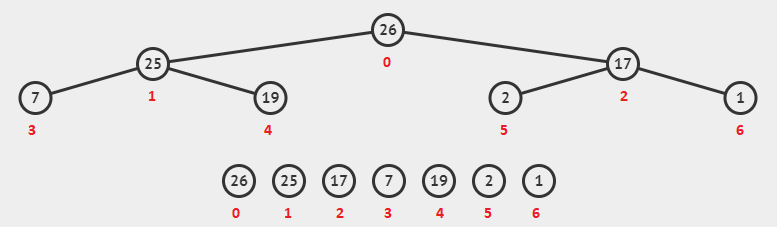
위의 그림에서 0번 인덱스를 이용하여 2n+1과 2n+2를 계산하면 자식노드의 인덱스인 1과 2를 구할수 있다. 이진힙은 이를 이용하여 구현해준다.
class MaxBinaryHeap {
constructor() {
this.values = [];
}
}기본 클래스의 구조는 위와 같다. 노드들의 집합으로는 배열을 사용하였으며, 배열을 사용하지 않고 따로 Queue구조를 만들어 더 효율적으로 사용할수도 있다.
insert() 삽입 메소드

최대 이진 힙에 어떤 데이터를 추가할때 일단 배열의 맨 끝에 데이터를 추가한 다음 버블업 단계를 거친다.
버블업이란 해당 값이 최대 이진힙에 들어가야 할 알맞은 장소를 찾을때까지 부모노드와 계속해서 비교해주며 자리를 바꿔주는 과정이다.
insert(val) {
if (!val) return undefined;
this.values.push(val);
this.bubbleUp();
}
bubbleUp() {
let currentIdx = this.values.length - 1;
let currentValue = this.values[currentIdx];
while (currentIdx > 0) {
let parentIdx = Math.floor((currentIdx - 1) / 2);
let parentValue = this.values[parentIdx];
if (currentValue <= parentValue) break;
this.values[parentIdx] = currentValue;
this.values[currentIdx] = parentValue;
currentIdx = parentIdx;
}
}- insert() 메소드가 호출되면 받은 인자값을 배열의 맨 끝에 추가해준뒤 버블업 메소드를 호출한다.
- 버블업에서는 배열에 새로 추가된 값과 그의 인덱스를 변수로 저장한다.
- 반복문을 사용하여 부모의 값과 자신의 값을 비교하며 자신의 값이 더 크다면 인덱스를 이용하여 위치를 바꿔준다.
- 이후 바뀐 인덱스를 현재의 인덱스에 저장하며 부모의 값이 자신보다 크거나 root의 인덱스에 도달할때까지 반복해 수행한다.
extractMax() 최대값 제거 메소드

현재트리의 최대값인 root를 제거하며 이후 배열의 마지막 데이터를 배열의 처음으로 옮긴뒤 버블다운 과정을 거친다.
버블다운이란 버블업과 반대로 root부터 시작해 자신의 자식노드와 비교하며 알맞은 자리를 찾아주는 과정이다.
버블다운 과정중에서 몇가지의 경우의 수가 생긴다.
1. 자신의 노드에 두 자식노드가 모두 없는경우
2. 첫번째 자식노드의 값이 두번째 자식노드의 값보다 큰경우
2-1. 그리고 첫번째 자식노드의 값이 현재노드의 값보다 작은경우
2-2. 또는 큰경우
3. 반대의 상황인 두번째 자식노드의 값이 첫번째 자식노드의 값보다 큰경우
3-1. 그리고 두번째 자식노드의 값이 현재노드의 값보다 작은경우
3-2. 또는 큰경우
4. 두번째 자식노드가 없는경우
extractMax() {
let removedMax = this.values[0];
let lastValue = this.values.pop();
if (this.values.length > 0) {
this.values[0] = lastValue;
this.bubbleDown();
}
return removedMax;
}
bubbleDown() {
let currentIdx = 0;
let currentValue = this.values[currentIdx];
while (true) {
let firstChildIdx = 2 * currentIdx + 1;
let firstChildValue = this.values[firstChildIdx];
let secondChildIdx = 2 * currentIdx + 2;
let secondChildValue = this.values[secondChildIdx];
if (!firstChildValue && !secondChildValue) return;
if (firstChildValue > secondChildValue) {
if (firstChildValue < currentValue) return;
this.values[currentIdx] = firstChildValue;
this.values[firstChildIdx] = currentValue;
currentIdx = firstChildIdx;
} else if (firstChildValue < secondChildValue) {
if (secondChildValue < currentValue) return;
this.values[currentIdx] = secondChildValue;
this.values[secondChildIdx] = currentValue;
currentIdx = secondChildIdx;
} else if (!secondChildValue) {
if (firstChildValue < currentValue) return;
this.values[currentIdx] = firstChildValue;
this.values[firstChildIdx] = currentValue;
currentIdx = firstChildIdx;
}
}
}- extractMax() 메소드 호출후 배열의 첫 아이템인 root를 반환해주며 마지막 데이터를 root로 옮겨준뒤 버블다운 메소드를 호출한다.
- 바뀐 데이터위치인 root의 인덱스와 데이터의 값을 변수에 저장한뒤 반복문안에서 그의 두 자식노드의 정보 모두 변수에 저장한다.
- 모든 자식노드가 없는경우, 즉 자신이 leaf인 경우 아무런 변화 없이 메소드를 종료한다.
- 첫번째 노드의 값이 두번째 보다 크지만 그의 부모노드보다는 작을경우 그대로 메소드를 종료, 만약 그의 부모노드보다 큰경우 서로의 위치를 바꿔주고 비교대상인 현재 노드의 인덱스 또한 바꿔주며 반복문을 계속해서 돌려준다.
- 두번째 노드의 값이 첫번째보다 클경우 마찬가지로 위와 동일하게 진행
- 만약 두번째 자식노드가 없다면 첫번째 자식노드와 부모노드만을 비교하며 동일하게 진행한다.
Priority Queue (우선순위 큐)
이진힙과 비슷하며 각각의 데이터가 우선순위에 대한 정보를 담고 이진힙의 로직을 이용하여 우선순위를 비교하는 자료구조를 만든다.
수도코드(pseudocode)는 위에 작성된 이진힙 코드와 매우 흡사하다. 각 데이터의 값과 우선순위 정보를 담을 노드를 생성시킬 클래스 작성, 노드의 값이아닌 우선순위를 비교하도록 변경, 변수 및 메소드의 이름 변경, 최대 이진힙이아닌 최소 이진힙으로 변경 등 사소한 차이만 있으므로 코드에대한 리뷰는 생략함.
class Node {
constructor(val, priority) {
this.value = val;
this.priority = priority;
}
}
class PriorityQueue {
constructor() {
this.values = [];
}
enqueue(val, priority) {
if (!val || !priority) return undefined;
let newNode = new Node(val, priority);
this.values.push(newNode);
this.bubbleUp();
}
bubbleUp() {
let currentIdx = this.values.length - 1;
let currentNode = this.values[currentIdx];
while (currentIdx > 0) {
let parentIdx = Math.floor((currentIdx - 1) / 2);
let parentNode = this.values[parentIdx];
if (currentNode.priority >= parentNode.priority) break;
this.values[parentIdx] = currentNode;
this.values[currentIdx] = parentNode;
currentIdx = parentIdx;
}
}
dequeue() {
let removedRoot = this.values[0];
let lastValue = this.values.pop();
if (this.values.length > 0) {
this.values[0] = lastValue;
this.bubbleDown();
}
return removedRoot;
}
bubbleDown() {
let currentIdx = 0;
let currentNode = this.values[currentIdx];
while (true) {
let firstChildIdx = 2 * currentIdx + 1;
let firstNode = this.values[firstChildIdx];
let secondChildIdx = 2 * currentIdx + 2;
let secondNode = this.values[secondChildIdx];
if (!firstNode && !secondNode) return;
if (secondNode && firstNode.priority < secondNode.priority) {
if (firstNode.priority > currentNode.priority) return;
this.values[currentIdx] = firstNode;
this.values[firstChildIdx] = currentNode;
currentIdx = firstChildIdx;
} else if (secondNode && firstNode.priority > secondNode.priority) {
if (secondNode.priority > currentNode.priority) return;
this.values[currentIdx] = secondNode;
this.values[secondChildIdx] = currentNode;
currentIdx = secondChildIdx;
} else if (!secondNode) {
if (firstNode.priority > currentNode.priority) return;
this.values[currentIdx] = firstNode;
this.values[firstChildIdx] = currentNode;
currentIdx = firstChildIdx;
}
}
}
}위의 코드에서는 각 노드의 우선순위가 같을경우는 고려하지 않았으며 만약 구현을 하게 된다면 각 노드에 시간정보 혹은 대기열 정보를 저장해준다음 우선순위가 같을경우 다른 정보또한 비교해주며 정렬해준다면 해결될것으로 보인다.
Big O notation
이진 힙과 우선순위 큐 모두 삽입과 제거에 대해 O(log n)의 시간 복잡도를 가지며 굉장히 좋은 성능을 보인다.
일반적인경우 [7,6,5,4,3,2,1]과 같은 배열이 주어지고 새로운 데이터 8을 추가해주게되면 8은 배열의 맨끝에 추가되고 내림차순으로 숫자 1번부터 7번까지 모든 수를 비교하게되지만 이진 힙을 사용하게되면 그의 부모값들인 4, 6, 7의 값들만을 비교하면 되므로 O(log n)이라는 결과가 나온다.
삭제의 경우도 마찬가지로 자식노드들과 비교하여 한칸씩 내려갈때마다 비교해야되는 데이터의 양은 이론적으로 1/2씩 줄어들게 된다.
또한 이진 탐색 트리의 경우 데이터들이 극단적으로 주어젔을때 트리의 형태가 마치 연결리스트와 같은 형태가 되며 최악의 시간복잡도는 O(n)이 되지만 이진 힙의 경우 트리의 형태가 언제나 균형잡혀 있기 때문에 최악의 경우에도 O(log n)을 유지한다. 하지만 이진 힙은 모든 노드들이 잘 정렬된 상태가 아니기 때문에 탐색을 목적으로 사용을할경우 높은 효율을 보여주지 않으며 탐색 알고리즘이 중요한 경우 다른 자료구조를 이용하는 것이 좋다.
'Datastructure & Algorithm' 카테고리의 다른 글
| 그래프 순회 (DFS, BFS) (0) | 2023.03.20 |
|---|---|
| 그래프 (Graphs) (0) | 2023.03.19 |
| Tree Traversal (트리 순회), BFS, DFS (0) | 2023.02.08 |
| Binary Search Tree (이진 검색 트리) (0) | 2023.02.08 |
| Stack & Queue 자료구조 (0) | 2023.02.01 |